
Informasjon
Hertz og Cent
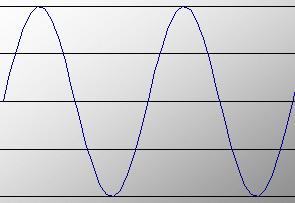
En tone som eksisterer av nøyaktig en frekvens ser ut som en sinusbølge:
Hertz
Plassen av en slik tone uttrykkes i Hertz: Antall bølger per sekund. I figuren over er to bølger vist.

Hertz
Plassen av en slik tone uttrykkes i Hertz: Antall bølger per sekund. I figuren over er to bølger vist.
Cent
Notene i skalaen (like temperament) øker i frekvens. Hver oktav består av 12 notater (semitoner) og tilsvarer en dobling i frekvens. A4 er 440 Hz og A5 880 Hz. Frekvensområdet (bredde) til et notat er derfor større hvis tonehøyde er høyere. A4 går fra 428 til 453 Hz og A5 går fra 855 til 906 Hz. Bredden på en halvton er per definisjon (alltid) 100 Cent.
Forholdet mellom Cent og Hertz
Bredden på en tone i Hertz øker ettersom stigningen øker. Bredden på en halvton i Cent er alltid 100. Forskjellen i Cent Δ mellom to toner med frekvensene f1 og f2 (i Hertz) kan beregnes som følger:
∆ = 1200 log2 (f1 / f2)
Hvis frekvensforskjellen (f2 - f1 i Hertz) øker lineært, øker forskjellen i Cent logaritmisk.
Avviket av en målt tone i Cent
Hvis tuneren viser en feil på en målt tone i Cent, betyr en feil på 0 Cent at tonen er helt riktig. Hvis avviket er -50 Cent, er den målte tonen akkurat midt i ønsket tone og forrige halvton. Hvis avviket er +50 cent, er den målte tonen akkurat i midten av ønsket tone og neste halvton.
Notene i skalaen (like temperament) øker i frekvens. Hver oktav består av 12 notater (semitoner) og tilsvarer en dobling i frekvens. A4 er 440 Hz og A5 880 Hz. Frekvensområdet (bredde) til et notat er derfor større hvis tonehøyde er høyere. A4 går fra 428 til 453 Hz og A5 går fra 855 til 906 Hz. Bredden på en halvton er per definisjon (alltid) 100 Cent.
Forholdet mellom Cent og Hertz
Bredden på en tone i Hertz øker ettersom stigningen øker. Bredden på en halvton i Cent er alltid 100. Forskjellen i Cent Δ mellom to toner med frekvensene f1 og f2 (i Hertz) kan beregnes som følger:
∆ = 1200 log2 (f1 / f2)
Hvis frekvensforskjellen (f2 - f1 i Hertz) øker lineært, øker forskjellen i Cent logaritmisk.
Avviket av en målt tone i Cent
Hvis tuneren viser en feil på en målt tone i Cent, betyr en feil på 0 Cent at tonen er helt riktig. Hvis avviket er -50 Cent, er den målte tonen akkurat midt i ønsket tone og forrige halvton. Hvis avviket er +50 cent, er den målte tonen akkurat i midten av ønsket tone og neste halvton.


























