
Information
Hertz and Cent
A tone which exists of exactly one frequency looks like a sine wave:
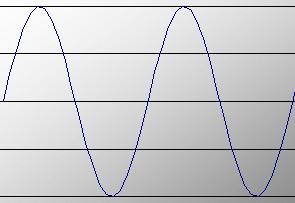
Hertz
The pitch of such a tone is expressed in Hertz: the number of waves per second. In the figure above two waves are shown.

Hertz
The pitch of such a tone is expressed in Hertz: the number of waves per second. In the figure above two waves are shown.
Cent
The notes in the scale (equal temperament) increase in frequency. Every octave exists of 12 notes (semitones) and corresponds to a doubling in frequency. The A4 is 440 Hz and the A5 880 Hz. The frequency range (width) of a note is therefore larger if the pitch is higher. The A4 runs from 428 up to 453 HZ and the A5 runs from 855 up to 906 Hz. The width of a semitone is by definition (always) 100 Cent.
The ratio between Cent and Hertz
The width of a tone in Hertz increases as the pitch increases. The width of a semitone in Cent is always 100. The difference in Cent ∆ between two tones with frequencies f1 and f2 (in Hertz) can be calculated as follows:
∆ = 1200 log2 (f1 / f2)
If the frequency difference (f2 - f1 in Hertz) increases linearly then the difference in Cent increases logarithmic.
The deviation of a measured tone in Cent
If the tuner shows an error of a measured tone in Cent, then an error of 0 Cent means that the tone is exactly right. If the deviation is -50 Cent then the measured tone is exactly in the middle of the desired tone and the previous semitone. If the deviation is +50 Cent then the measured tone is exactly in the middle of the desired tone and the next semitone.
The notes in the scale (equal temperament) increase in frequency. Every octave exists of 12 notes (semitones) and corresponds to a doubling in frequency. The A4 is 440 Hz and the A5 880 Hz. The frequency range (width) of a note is therefore larger if the pitch is higher. The A4 runs from 428 up to 453 HZ and the A5 runs from 855 up to 906 Hz. The width of a semitone is by definition (always) 100 Cent.
The ratio between Cent and Hertz
The width of a tone in Hertz increases as the pitch increases. The width of a semitone in Cent is always 100. The difference in Cent ∆ between two tones with frequencies f1 and f2 (in Hertz) can be calculated as follows:
∆ = 1200 log2 (f1 / f2)
If the frequency difference (f2 - f1 in Hertz) increases linearly then the difference in Cent increases logarithmic.
The deviation of a measured tone in Cent
If the tuner shows an error of a measured tone in Cent, then an error of 0 Cent means that the tone is exactly right. If the deviation is -50 Cent then the measured tone is exactly in the middle of the desired tone and the previous semitone. If the deviation is +50 Cent then the measured tone is exactly in the middle of the desired tone and the next semitone.























