
Información
Hertz y Cent
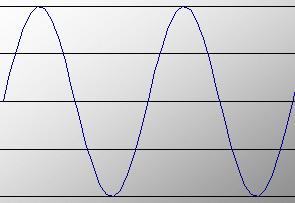
Un tono que existe exactamente, una frecuencia se parece a una onda sinusoidal:
Hertz
La altura de un sonido se expresa en Hertz: el número de ondas por segundo. En la figura se muestran por encima de dos ondas.

Hertz
La altura de un sonido se expresa en Hertz: el número de ondas por segundo. En la figura se muestran por encima de dos ondas.
Cent
Las notas de la escala (temperamento igual) aumentan en frecuencia. Cada octava existe de 12 notas (semitonos) y corresponde a una duplicación de la frecuencia. El A4 es de 440 Hz y la A5 880 Hz. Por tanto, el rango de frecuencias (ancho) de una nota es más grande si el tono es más alto. El A4 va desde 428 hasta 453 Hz y la A5 va desde 855 hasta 906 Hz. El ancho de un semitono, por definición es (siempre) 100 Cent.
La relación entre Cent y Hertz
El ancho de un tono en hercios aumenta a medida que aumenta de tono. El ancho de un semitono en Cent es siempre 100. La diferencia en Cent Δ entre dos tonos con frecuencias f1 y f2 (en Hertz) se puede calcular de la siguiente manera:
∆ = 1200 log2 (f1 / f2)
Si la diferencia de frecuencia (f2 - f1 en Hz) aumenta linealmente entonces la diferencia de Cent incrementos logarítmicos.
La desviación de un tono medido en Cent
Si el afinador muestra un error de un tono mesurado de Cent, a continuación, un error de 0 Cent significa que el tono es exactamente correcto. Si la desviación es de -50 Cent entonces el tono medido es exactamente en el medio del tono deseado y el semitono anterior. Si la desviación es +50 Cent entonces el tono medido es exactamente en el medio del tono deseado y el siguiente semitono.
Las notas de la escala (temperamento igual) aumentan en frecuencia. Cada octava existe de 12 notas (semitonos) y corresponde a una duplicación de la frecuencia. El A4 es de 440 Hz y la A5 880 Hz. Por tanto, el rango de frecuencias (ancho) de una nota es más grande si el tono es más alto. El A4 va desde 428 hasta 453 Hz y la A5 va desde 855 hasta 906 Hz. El ancho de un semitono, por definición es (siempre) 100 Cent.
La relación entre Cent y Hertz
El ancho de un tono en hercios aumenta a medida que aumenta de tono. El ancho de un semitono en Cent es siempre 100. La diferencia en Cent Δ entre dos tonos con frecuencias f1 y f2 (en Hertz) se puede calcular de la siguiente manera:
∆ = 1200 log2 (f1 / f2)
Si la diferencia de frecuencia (f2 - f1 en Hz) aumenta linealmente entonces la diferencia de Cent incrementos logarítmicos.
La desviación de un tono medido en Cent
Si el afinador muestra un error de un tono mesurado de Cent, a continuación, un error de 0 Cent significa que el tono es exactamente correcto. Si la desviación es de -50 Cent entonces el tono medido es exactamente en el medio del tono deseado y el semitono anterior. Si la desviación es +50 Cent entonces el tono medido es exactamente en el medio del tono deseado y el siguiente semitono.























